Part 2 : Transformers: Input Embedding and Positional Encoding
- aimlfastrace
- Jan 19
- 10 min read
Updated: Jan 24
Understanding Transformers: Input Embedding and Positional Encoding
Before reading this blog refer to Part 1 below to understand the different components of Transformers
Part 1 : Transformers: Introduction to the backbone of Generative AI - https://www.aiconnectgrow.com/post/part-1-transformers-introduction-to-the-backbone-of-generative-ai or refer the video https://youtu.be/acUX5uIJYVs
Youtube Video: You can refer the video link https://youtu.be/JQzlCrqTMLU for the detailed explanation of the blog.
Code using Pytorch for this blog: Youtube Video https://youtu.be/Ing1vzG9Rjk explains How to easily code Input Embedding and Positional Encoding in detail
Input Embedding and Positional Encoding:
Welcome to my blog! Today, I'll guide you through the essential building blocks of the Transformer, focusing on Input Embedding and Positional Encoding. We'll explore both the underlying theories and practical implementations using PyTorch. My goal is to break down the complex mechanics of Transformers, making each component clear and easy to understand.
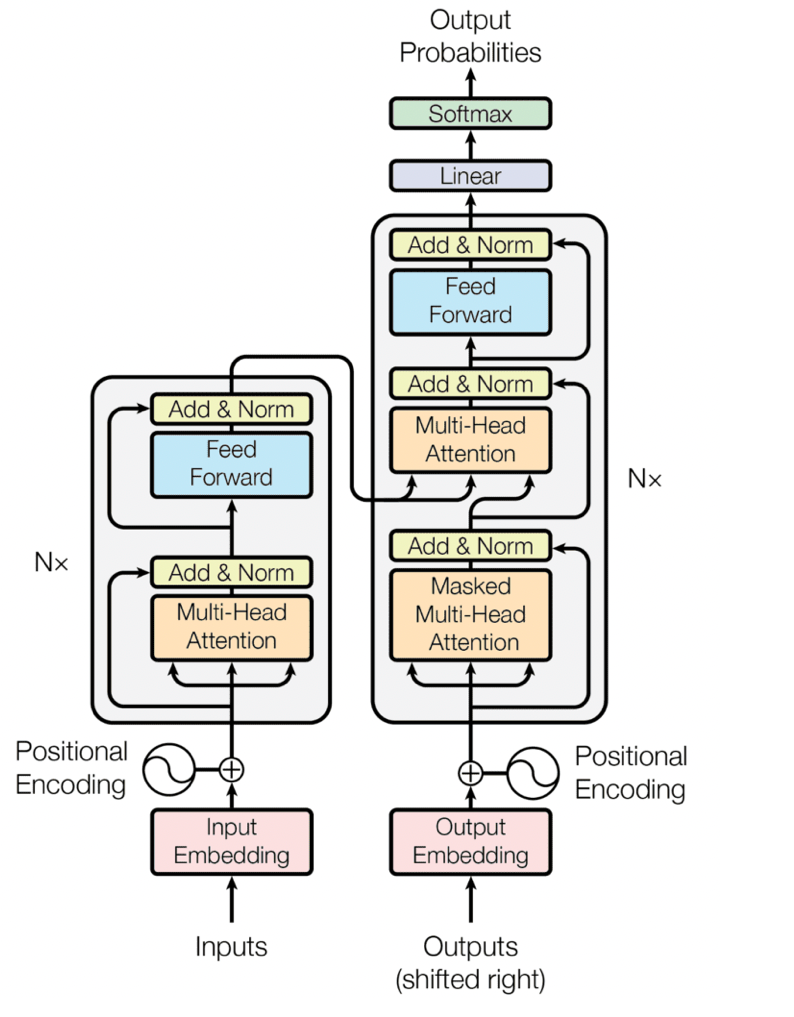
The initial step in any transformer model involves input embeddings and positional encoding. These two components work together to prepare the raw input data so the model can process it effectively.
Input embeddings are like a translator for the model. They convert words or tokens from the input sequence into dense vectors of numbers that the transformer can understand. These vectors represent not just the word itself but also capture its meaning and relationship to other words in the context of the sequence.
Positional encoding adds crucial information about the order of words in the sequence. Unlike humans, transformers don’t inherently understand the sequence of data since they process inputs all at once (in parallel). Positional encoding fills this gap, helping the model know which word comes first, second, and so on.
Together, input embeddings and positional encoding act as the foundation for the transformer. Without them, the model wouldn’t be able to grasp the meaning of the input or how the parts of the input relate to each other. Let’s now take a closer look at input embeddings to see how they work!
Let us dive into the minute details of Input Embedding and Positional Encoding. The image below illustrates how data is transformed by these layers. Once you have read the complete blog, you can refer back to this image to revise your concepts.
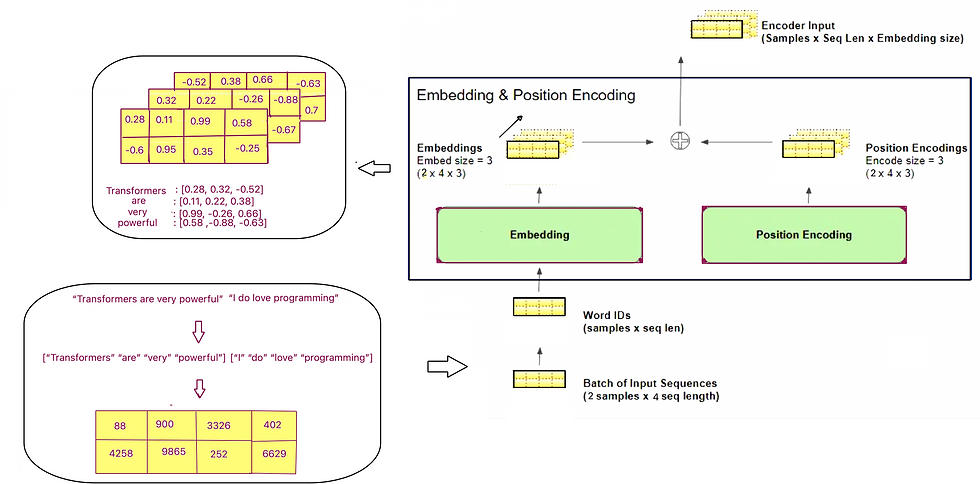
Input Embedding
In any deep learning model, input embeddings are used to convert raw data, such as words or tokens, into numerical representations that can be processed by the model. In the context of transformers, input embeddings are crucial because they translate each word or token in a sequence into a high-dimensional vector. This vector represents the meaning and semantic properties of the word in a way that the model can understand and manipulate.
Why Is It Needed?
The natural language is made up of words or tokens, and these individual pieces of data need to be transformed into a form that a machine learning model can process.The input embedding helps to convert each word into a vector, which the model can then use to perform tasks such as classification, translation, or generation.
For example, the word "cat" might be represented by a vector like [0.2, -0.5, 0.7]. This vector contains information that the model uses to understand the word’s relationship with other words in the sequence. The more advanced the embedding method, the more effectively it captures these semantic relationships.
How Does It Work?
In the Transformer model, the input embedding is typically created using pre-trained embeddings such as Word2Vec, GloVe, or even embeddings learned from scratch during training. Each word in the sequence is mapped to a vector of a fixed size. These vectors are learned in a way that similar words (like "dog" and "cat") will have embeddings that are closer in the vector space.
Here’s a breakdown of how input embedding works:
Tokenization: First, the input text is tokenized into smaller pieces (words, subwords, or characters).
Lookup Table: A lookup table, also called an embedding matrix, contains the embeddings for each token in the vocabulary. Each token is assigned an embedding vector, typically of high dimension (e.g., 512 or 1024)
Embedding Layer: The tokenized sequence is passed through an embedding layer that maps each token to its corresponding embedding vector from the lookup table.
Mathematics Behind It:

Key Features of Input Embedding:
Fixed Representation: Each token is mapped to a fixed-dimensional vector that remains constant throughout training and inference.
Learned during Training: The embeddings are initialized randomly and then fine-tuned during training to capture the nuances of the specific task the model is being trained for.
Semantic Similarity: Words with similar meanings tend to have similar embeddings, making it easier for the model to capture relationships between words.
PyTorch Code for Input Embedding
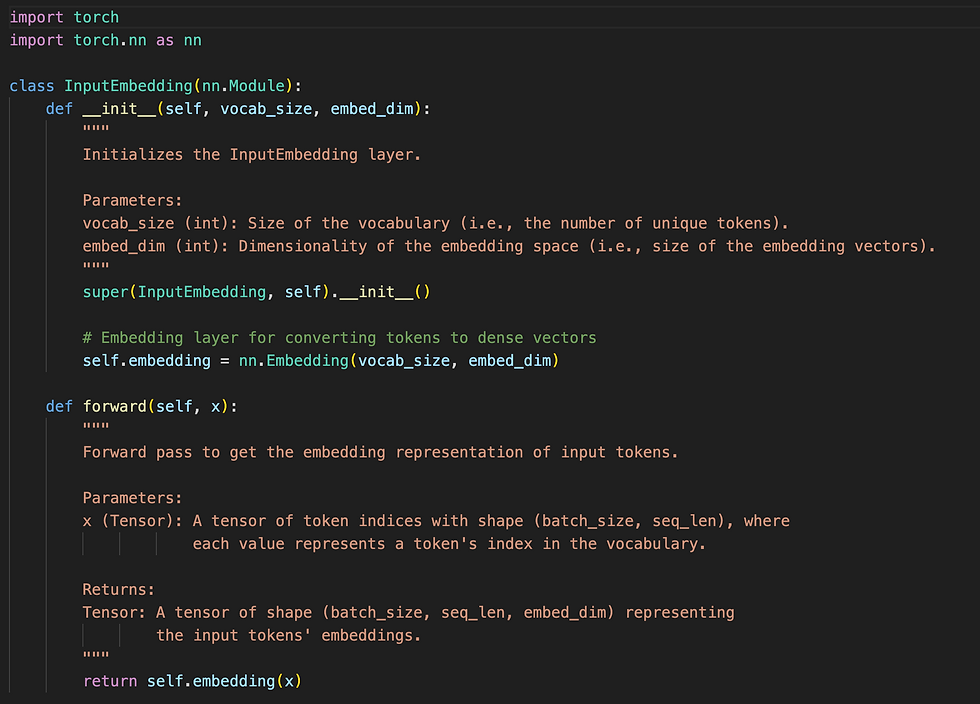
Explanation of the Code
InputEmbedding Class:
The class InputEmbedding inherits from nn.Module and contains an embedding layer (nn.Embedding) that is responsible for converting token indices into dense vectors.
The constructor init initializes the embedding layer, where vocab_size is the number of unique tokens, and embed_dim is the size of the embedding vectors.
Forward Method:
The forward method takes an input tensor x (of shape (batch_size, seq_len)) containing token indices. It then returns the corresponding embeddings of shape (batch_size, seq_len, embed_dim) by passing x through the embedding layer.
Example Usage:

The code demonstrates how to instantiate the InputEmbedding class and use it to transform a batch of tokenized sequences into embeddings.
vocab_size: Represents the size of your vocabulary. For example, if you have 10,000 unique tokens in your text corpus, set this to 10000.
embed_dim: Defines the size of the dense embedding vectors. This is typically a hyperparameter (e.g., 128, 256, 512).
example_input: A tensor where each row represents a sequence of token indices. Each value in the tensor corresponds to a token's index in the vocabulary.
Output: The output_embeddings tensor will have a shape of (batch_size, seq_len, embed_dim)(e.g., 2, 3, 512)
Input Embedding Input / Output Tensor Dimensions
The dimension of the input and output tensors for the Input Embedding example can be described as follows:
Input Tensor Dimensions
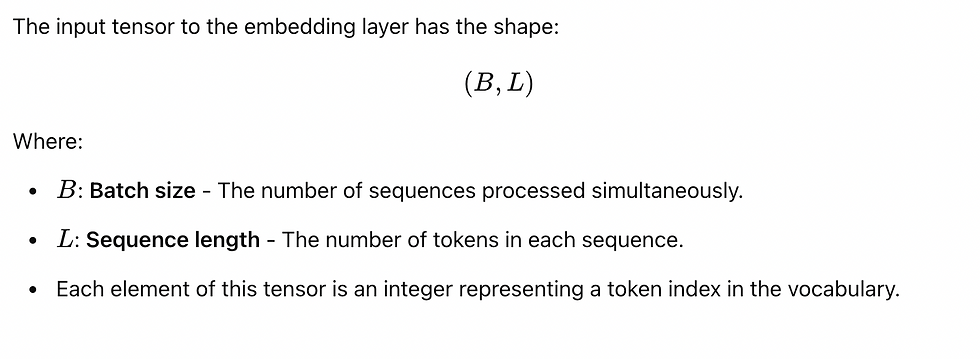
Thus, in the above example the input tensor shape is:(N, T) = (2, 3) — A batch of 2 sequences, each containing 3 tokens.
Output Tensor Dimensions

Thus, in the above example the output tensor shape is:(N, T, D) = (2, 3, 512) — The batch size remains 2, the sequence length remains 3, but each token is now represented by a 512-dimensional vector.
Sample Input and Output
Raw Text:
["I love programming", "Transformers are powerful"]
This text would be tokenized into the following indices based on the vocabulary of the model:
Sample Input (Token Indices):
tensor([[6542, 8882, 8341], # Token indices for the first sentence
[8972, 3651, 9371]]) # Token indices for the second sentence
Output Embeddings (Shape)
After passing the input tensor through the InputEmbedding layer, the output tensor will have the shape (2, 3, 512), as explained above.
Output Embeddings (Values)
The actual output tensor, which contains the embedding vectors for each token, will look like this (values are randomly initialized for illustration purposes):
tensor([[[ 1.1783, -0.4895, 1.2987, ..., -0.2909, -0.1299, -1.4825],
[ 0.7400, 0.2925, 1.4605, ..., -0.9125, 0.8454, -0.3570],
[ 0.2104, 0.6715, -0.2358, ..., 0.1131, -0.3567, 0.5761]],
[[ 0.3729, 0.1159, 0.6355, ..., -0.5798, 1.2385, 0.0199],
[-0.7880, -0.0142, -0.0356, ..., -0.3110, -0.2363, 0.7364],
[-0.3859, -0.2320, 0.1284, ..., 0.0567, 0.5954, -0.1985]]])
Key Points:
Input Tensor: Contains the token indices for a batch of sequences.
Output Tensor: Contains the embeddings corresponding to each token index. Each token is represented as a 512-dimensional vector.
Github Input Embedding Sample code:
Positional Encoding
In simple terms, positional encoding is a clever trick used in Transformer models to help them understand the order of words in a sequence, such as in a sentence. Unlike RNNs or LSTMs, which process words sequentially and naturally capture word order whereas Transformers process all words in parallel. This parallel processing means the model lacks a built-in sense of the order of words. Positional encoding solves this problem by adding information about the position of each word in the sequence, enabling the Transformer to understand the structure and meaning of the input.
Why Is It Needed?
Imagine trying to understand the sentence "I love programming" without knowing which word comes first, second, or last. In a Transformer model, positional encoding solves this problem by adding some extra information about the position of each word in the sequence.
How Does It Work?
Positional encoding uses sine and cosine functions to generate a unique signal for each word's position. Here’s a breakdown:
Position as a Number: First, each position in the sequence is assigned a number (like 0 for the first word, 1 for the second, and so on).
Sine and Cosine Waves: For each position, a sine wave is used for the even-numbered dimensions, and a cosinewave for the odd-numbered dimensions. These waves are special because they allow us to measure the difference between positions in a continuous way — meaning we can understand both absolute positions (where is the word in the sentence?) and relative positions (how far apart are two words?).
Mathematics Behind It:
The positional encoding is defined using sine and cosine functions as follows:
For each position p (ranging from 0 to max_len−1) and each dimension i of the embedding vector (ranging from 0 to embed_dim−1):

Where:
p is the position of the token in the sequence (starting from 0),
i is the dimension of the embedding vector,
dmodel is the embedding dimension.
The terms 2i and 2i+1 indicate that even indices are associated with sine values, and odd indices with cosine values. This alternating pattern helps the model differentiate between positions at different embedding dimensions.
Intuition Behind the Formula
Scaling: The term 10000*(2i/dmodel) is used to scale the position values so that they vary in a smooth and consistent manner across different dimensions. The lower-dimensional sine and cosine functions oscillate faster for smaller indices, while the higher-dimensional ones oscillate more slowly.
Sine and Cosine Functions: The sine and cosine functions are periodic, meaning that the position encoding values will repeat after a certain number of positions. This periodicity allows the model to "learn" positions relative to each other (e.g., knowing that position 0 is far from position 3, etc.)
Key Features of Positional Encoding:
No learnable parameters: Positional encoding is a fixed function of the position and dimension, which makes it easy to implement.
Continuous and smooth: The sine and cosine functions create smooth variations, allowing the model to compute relative positions.
Compatibility with any sequence length: The model can process sequences of any length by adjusting the positional encoding tensor appropriately.
PyTorch Code for Positional Encoding
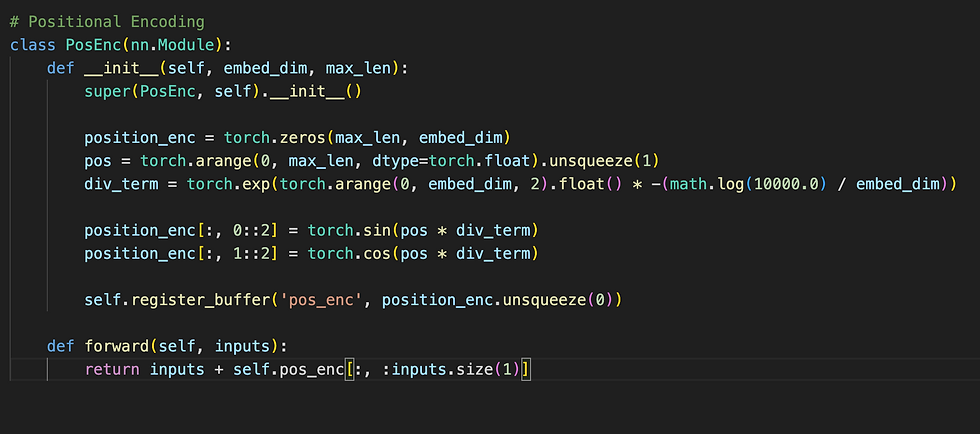
Explanation of the Code
1. Class Initialization (__init__ Method)
Parameters:
embed_dim: The dimension of the embedding vector (e.g., 512). It determines how many values represent each position in the sequence.
max_len: The maximum sequence length. It specifies the maximum number of tokens the model can handle in one sequence.
Steps:
Creates a zero tensor to hold the positional encodings:
This tensor will eventually store the sine and cosine values for all positions and embedding dimensions.
Defines the positions of tokens:
torch.arange(0, max_len): Creates a tensor [0, 1, 2, ..., max_len-1] representing token positions.
.unsqueeze(1): Adds a second dimension to make it a column vector of shape (max_len, 1).
Calculates the divisors for sine and cosine functions:
torch.arange(0, embed_dim, 2): Creates indices [0, 2, 4, ...] for even dimensions.
-(math.log(10000.0) / embed_dim): Scales the embedding dimensions exponentially.
torch.exp(...): Applies the exponential function to generate the divisors for encoding.
Assign sine to even indices and cosine to odd indices:
0::2: Selects even indices.
1::2: Selects odd indices.
pos * div_term: Combines position and divisor to calculate the sine and cosine values.
Register the positional encoding as a buffer:
unsqueeze(0): Adds a batch dimension to make the tensor shape (1, max_len, embed_dim).
register_buffer: Stores the positional encoding as part of the model but excludes it from training (i.e., it's not a trainable parameter).
2. Forward Pass
Input:
inputs: A tensor of input embeddings with shape (batch_size, seq_len, embed_dim).
Steps:
Add positional encoding to the input embeddings:
self.pos_enc[:, :inputs.size(1)]: Slices the positional encodings to match the sequence length (seq_len) of the input.
inputs + : Adds the positional encodings to the input embeddings element-wise.
Output:
The output is a tensor of shape (batch_size, seq_len, embed_dim) with positional encodings added to the input embeddings.
Positional Encoding Input / Output Tensor Dimensions:
The dimension of the input and output tensors for the positional encoding example can be described as follows:
Input Tensor Dimensions
The input tensor provided to the PosEnc class has dimensions:
Batch size (N): Number of sequences in a batch. In this example, it is 2.
Sequence length (T): Length of each sequence. In this example, it is 4.
Embedding dimension (D): Size of the embedding vector for each token in the sequence. In this example, it is 6.
Thus, the input tensor shape is: (N,T,D)=(2,4,6)(N,T,D)=(2,4,6)
Output Tensor Dimensions
The output tensor produced by the PosEnc class has the same dimensions as the input tensor, as the positional encoding is added element-wise to the input tensor. Therefore, the output tensor shape is also: (N,T,D)=(2,4,6)(N,T,D)=(2,4,6)
Summary
Input tensor dimensions: (2,4,6)(2,4,6)
Output tensor dimensions: (2,4,6)(2,4,6)
The positional encoding layer does not change the shape of the tensor; it only adds positional information to the existing embeddings.
Positional Encoding Sample Input and Output :
Input Parameters:
Sequence length (S) = 4
Batch size (B) = 2
Embedding dimension (d) = 6
Steps:
Positional Encoding Calculation: We compute the positional encodings for a sequence of length 4. The embedding dimension is 6, so we generate 6 positional encoding values for each position.
Shape of Positional Encoding: For a batch size of 2, the shape of the positional encoding matrix would be (B, S, d), i.e., (2, 4, 6).
Sample Input
Sample Input Tensor (Shape: (2, 4, 6)): (from input embedding)
tensor([[[-0.8513, -1.1051, 1.0712, -0.6826, 0.5432, 0.1897],
[ 0.4081, 0.7527, 1.2853, -0.0842, 0.3564, -1.6070],
[ 0.4850, 0.8720, 0.8326, -1.6016, 0.0184, -0.2214],
[-0.0454, -0.3287, -0.3017, 0.3715, -0.7881, -1.0301]],
[[ 0.3276, -1.5497, 0.1396, 0.3583, 1.4391, 1.6798],
[-0.0584, 0.1285, -1.5946, -1.1017, -0.3425, -0.5582],
[-0.2654, 0.7975, 0.5505, -1.4156, -0.8361, 0.1532],
[ 0.0812, -0.1763, -0.1225, 0.4071, 0.9467, -0.6651]]])
Output with Positional Encoding
To incorporate the positional encoding with the input tensor, we simply add the positional encoding to the input tensor. This results in the final representation, which contains both the original token embeddings and the position-related information.
The shape of the output matrix would be the same as input matrix (2, 4, 6) with each row showing the positional encoding for each token in the sequence.
tensor([[[-0.8513, -0.1051, 1.0712, 0.3174, 0.5432, 1.1897],
[ 0.4081, 1.7527, 1.2853, 0.9158, 0.3564, -0.6070],
[ 0.4850, 1.8720, 0.8326, -0.6016, 0.0184, 0.7786],
[-0.0454, 0.6713, -0.3017, 1.3715, -0.7881, -0.0301]],
[[ 0.3276, -0.5497, 0.1396, 1.3583, 1.4391, 2.6798],
[-0.0584, 1.1285, -1.5946, -0.1017, -0.3425, 0.4418],
[-0.2654, 1.7975, 0.5505, -0.4156, -0.8361, 1.1532],
[ 0.0812, 0.8237, -0.1225, 1.4071, 0.9467, 0.3349]]])
In the output, each element of the input tensor has been modified by adding the corresponding positional encoding values, demonstrating how positional information is incorporated into the input data.
This final output tensor can now be passed on to the next layers of the transformer model. These layers will use both the token's actual information and its position in the sequence to understand the relationships between tokens, making it great for tasks like translation or text classification.
In my upcoming blog, I'll dive deeper into the next exciting step: multi-head attention, which takes this process even further! Stay tuned to learn how it helps the model focus on different parts of the input sequence at once.


Comments